Transaction management：可串行性（serializability）

距离上次更新已经很久了，过年的这段时间刚好是学期中，重度拖延症拖下来的projects和midterms堆在一起，实在忙得不可开交。这个周末闲下来一点，眼看着又一次写博客的尝试又要半途而废，就抽出时间来总结记录一下最近的学习历程和心得吧。这一篇文章以及后续（可能会有）的一系列文章会简单介绍一下数据库事务管理（database transaction management）和分布式数据管理（distributed data management）。

前言

我们可能没有意识到，数据库已经渗透到我们生活中的点点滴滴，无处不在：早上起床打开手机放一首喜欢的歌，播放器需要访问数据库调取歌曲信息；出门到银行取钱，账户和交易信息都由银行的数据库保存和处理；晚上回到家打开网页浏览新闻，网站后台也一定会使用数据库…… 我们也很难意识到，这个系统究竟有多么复杂：想像你正在打一通美国到中国的跨洋长途电话，你的拨号请求会被附近你的服务商基站处理，并找出一条到中国目的基站的线路。这条线路会途径许多层级的电话线路交换机。为了计算费用，每一处都有相应的数据库记录线路连接的数据，比如时长信息等等。更复杂的是，这样规模的电话线路肯定不会为一家电信服务商单独所有，电信服务商也会租用第三方线路提供商提供的线路，这些提供商也要根据线路使用情况向电信服务商收费。在你拨通太平洋另一端的电话号码的短短几秒钟内，十几家公司的上百个数据库被同时调动、十几个不同的计费信息开始处理，要是电话没能接通，这些数据也应当被相应地取消…… 作为一个程序员，单单是想像正确地实现这样一次通话的数据处理都觉得复杂到头疼，更别提现实情景中，这样一个数据库每秒需要并行处理上万次通话了。

然而这样复杂的一个系统，还对正确性有非常苛刻的要求。没人希望自己被一通没有拨通的长途电话收费，也没人会接受一笔银行转账扣了钱却不知所踪。在其他领域，保证正确性的做法通常是牺牲一部分的性能，但是在数据库的很多使用场景中，每秒能够处理的请求数量也非常关键，尤其是之前提到过的国际长途或者互联网之类的全球性服务，牺牲了高并行的性能甚至可能完全无法使用。

综上所述，如何在大规模、甚至分布在全球的数据库系统中保证高度并行处理中的正确性，绝对不是一个琐碎容易（trivial）的问题。希望以上的介绍和例子能够成功勾起读者的兴趣和注意。这个问题也许在当今的计算机科学研究中没有很大热度，但它还是非常有趣，也有很高的实用价值。如果不能清楚地了解问题是什么就没法给出优秀的解决方案，所以这篇文章还不会跳到具体的算法和实现，我们先简单了解一下如何为这个问题建立模型。

问题模型

在开始之前我觉得有必要给大家提醒一下这一篇文章和后续（可能会有）的一系列文章所讨论的范畴：尽管我们感兴趣的这个问题是一个工程上的实际问题，但是为了更好的理解它的性质我们还是要从简化抽象的理论分析开始。所以我们在这一节里提出的模型跟现实世界有一些落差。我们会先定义什么是一个数据库以及在数据库上的操作；基于这个数据库的模型，我们会介绍事务（transaction）和调度（schedule）的概念。

还有一点题外话，鉴于我学习这些概念的时候就是学的英文，而且我个人觉得有些概念的中文翻译不是很到位（事务是什么鬼啊喂！），我还是习惯在提及这些概念的时候使用英文。对，没错，我就是词汇匮乏，看不惯中英夹杂的中文警察可以散了。

我们的目标 没有蛀牙！

不知道目的地就不能合理地规划路线，不清楚追求的目标就没法设计出正确的算法。在一切分析开始之前，我们先来仔细思考一下我们的目的是什么、对于一个数据库系统来说，“正确性”意味着什么。

从直觉上说，一个数据库就是用来保存数据，那只要数据能按我们的预期被读取写入并且不出错，这个数据库就可以被认为是“正确”的。那“数据不出错”又意味着什么呢？这个简单问题的答案并不是非常显然。从语义上（syntactic）来看，一条数据拥有一个值，但是这个值是什么并没有具体的要求。但是大部分人很可能会认为存入一百块钱钱之后银行账户余额变成了负数并不正确。于是我们发现，数据库的正确性实际上跟context有关，不同的数据库可能会有不同的constraints。比如在机票预订或者座位预订系统中，我们会要求剩余票数或者座位数不能小于零；在银行转账中转账双方账户总额应当不变等等。这样的正确性要求看起来似乎很简单，但是在并行的情况下就没这么简单了。举个例子：程序A想要从账户x转一百块钱到账户y；程序B想要计算账户x和账户y的资产总额。假设账户x和账户y初始各有一千块钱。如果A和B并行执行，那么有可能B先读取了x的余额1000，然后A将100从x转到y，最后B又读取了y的余额1100，计算得出x+y=2100！一个正确的数据库系统应当避免这种情况的发生。

除了正确性之外，我们对数据库可能还有很多其他的要求，比如支持操作回滚等等。限于篇幅，这篇文章只讨论正确性，其他的内容会在后续（可能会有）的文章中讨论。

数据库模型

提到数据库，很多人的第一想法可能就是 SELECT ... FROM ... WHERE ... 的SQL语句。这样的关系数据库模型在现实系统中非常常见，但是读者之后可以看到，对于我们的分析来说这种模型并没有反映出数据库最底层最关键的不可分割的原子操作（atomic operations）。除此之外，这种基于关系的数据模型引入了我们不需要的概念：关系，在key-value store的数据库中我们同样会有正确性的问题。所以我们重新定义一个简化的数据库模型：

一个数据库系统由一个不可再分（indivisible）的、互不重叠（non-overlapping）的数据对象（data objects）的集合构成：$\{o_1, o_2,\dots,o_n\}$，每一个object都有一个取值范围（domain of values）。这个系统的一个状态（state） 就是一个从object到value的映射。数据库的操作有$read$（$r(o_i)$）和$write$（$w(o_i)$）。¹

简单来说，在这个模型中我们只关心最原始的、不可再分的数据的读和写，比如银行账户的余额，或者航班上的剩余座位。在这个模型中单独一条SQL语句也可能会被分拆成很多项操作。

数据库事务（database transactions）

Transaction 是对数据库系统中读写操作的更高一层抽象，代表了“一个单位”的数据库操作。一个transaction可能包含对多个数据对象的多个读写操作，但是这些操作被视为一个整体、一个“transaction”。举个例子，之前提到的银行转账涉及了分别读写x和y两个账户，在我们的数据库模型中可能被表示为 $r(x)~w(x)~r(y)~w(y)$，但是这四个操作应当被视为一个整体。

Transaction必须满足ACID特性¹²³：

• Atomicity: 一个transaction就是一个不可再分的单位操作，要么完全执行成功、要么完全不执行。如果transaction中的某一项读写操作失败了，那么整个transaction都应该失败，之前执行过的读写操作也应该回滚，整个系统应该恢复到执行这个transaction之前的状态。
• Consistency: 一个transaction应当使数据库从一个合法的状态变化到另一个合法的状态，保证数据正确性和完整性。在我们之前举的银行转账和计算总额的例子中，最终的状态就不合法，因为计算得出的总额并不正确，不满足银行账户这个数据库系统的implied constraints.
• Isolation: 并发执行的transactions不会观察到其他transactions执行中的中间结果或者说副作用（partial effects）。还是之前的银行转账的例子，导致数据不正确、consistency被破坏的原因就是A、B两个程序没有满足isolation，B看到了A的partial effect.
• Durability: 一旦一个transaction成功执行，那执行的结果就应当是（相对）永久性的。

Transaction这个概念放在数据库的使用情景中看非常自然，比如银行交易（transaction）本身就是一个transaction。ACID的要求也是现实生活中非常普遍的，比如预订联程航班时，要么就成功预订所有航段的机票、要么就一张机票都不预订。更加重要的是，transaction这个概念为数据库的用户和程序员提供了一层非常方便的抽象，用户只需要使用transaction来编写业务逻辑就可以享受其ACID性质，而不需要自己处理复杂的正确性需求。我个人认为这样的层层抽象（还比如网络的OSI多层模型）是计算机科学非常优雅的美感之一。

为了方便描述和使用transaction模型，这里给出正式定义¹：

一个transaction $T_i$是一个偏序$\prec_i$：

\[T_i\subseteq\{r_i(x), w_i(x)\mid x~\mathrm{is~an~object}\}\cup\{a_i, c_i\}\cup\{b_i\}\]

其中，$a_i$ 代表abort；$c_i$ 代表commit；$b_i$ 代表begin。$T_i$ 由 $b_i$ 开始，$a_i$ 和 $c_i$只能存在一个，并且是 $T_i$ 的最终操作。为了简洁，$b_i$ 和 $c_i$ 经常被省略。

如果操作 $o_i(x)$ 和 $o_i’(x)$ 属于 $T_i$，那要么 $o_i(x)\prec_i o_i’(x)$，要么 $o_i’(x)\prec_i o_i(x)$。

$T_i$ 中写操作 $w_i(x)$ 写入数据对象 $x$ 的值是一个关于 $T_i$ 之前（由 $\prec_i$ 定义）所有读取的值的函数。比如在 $T_1: r_1(x)~r_1(y)~w_1(z)$ 中，$z$ 的值是关于 $x$ 和 $y$ 的某个函数 $f(x, y)$，也就是说我们没有对写操作做任何假设，写入的值可能会取决于 $T_i$ 观察到的所有值。

事务调度（schedule）

明白了transaction的概念，理解schedule就很简单了：一个schedule就是多个transactions的交错，就是多个transaction中的多个数据操作用什么顺序执行的一个“计划”（或者执行过的历史，所以有时也叫history）。

最简单的schedule就是按顺序执行多个transactions：

类似这样的schedule叫做 serial schedule（串行调度）。Serial schedule在我们的分析中非常重要，但是就执行效率来说并不理想：如果 $T_2$ 被某个数据操作block了，那么等待数据的这段时间就会被浪费，从而增加了 $T_1$ 和 $T_3$ 的响应时间，所以schedule中不同的transaction很可能是交错执行的：

Schedule的正式定义是¹：

一个schedule $S=(\tau, \prec_S)$，其中：

• $\tau$ 是transaction的集合；
• $\prec_S$ 是 $\tau$ 中transactions中的数据操作的偏序，并满足： $\forall\,T_i\in\tau, \prec_i\subseteq\prec_S$，也就是说，schedule会保持每个transaction中操作自己的顺序。

可串行性（serializability）

简单来说，transaction就是具有意义的数据库操作最小单位，可能包含多个具体的数据读写操作；schedule描述了多个transaction如何穿插执行。有了基本的模型，我们的目标也更加明确了：如何得出高并发并且正确的schedule？或者在现实应用中由于复杂度和机能限制，如何辨别并拒绝错误的、可能会破坏数据consistency的schedule？

要回答这两个问题，我们首先需要回答“正确”对于schedule来说意味着什么（déjà vu!）。

直觉上分析，schedule可能出现的“错误”来源于多个transaction的并发执行。再回顾我们之前提到的银行转账的例子，在我们的模型中可以描述为：

在schedule $S$ 中，$T_B$ 读取了 $T_A$ 执行的中间结果，ACID中的isolation被破坏了，所以产生了inconsistent的结果。既然问题出在并发执行上，那我们确保顺序执行不就好了吗？在这个例子中，$S’: T_A~T_B$ 或者 $S’’: T_B~T_A$ 都可以保证结果的正确性。但是我们上文也提到，这样的serial schedule性能非常差，respond time和throughput都不理想，在某些应用中甚至完全不可用。但起码我们思考的方向是对的：我们既想要高并发的速度，又想要串行执行的isolation和正确性。那我们只需要保证一个schedule是“等价于”某个serial schedule的就行了，这就是 serializability（可串行性/化） 的概念¹⁴：

如果一个schedule $S=(\tau, \prec_S)$ 等价于 某个serial schedule $S’=(\tau, \prec_{S’})$，那么 $S$ 就是serializable（可串行）的。

那么问题又来了：对于两个schedule来说，什么叫做等价呢？这就是我们要讨论的关键问题了。接下来的几个小节会讨论三种不同的定义，并相应地得出 final state serializability、view serializability、和 conflict serializability 的概念。（我并没有找到这些概念合适的中文翻译，网络上的一些翻译在我感觉也不是很贴切，所以我斗胆自行翻译了这三个概念，但还是会主要使用英文原文。）

终态可串行（final state serializability）

提起“等价”的定义，我们可能首先会想到function中“external equivalence”的概念：把两个function当作黑盒，如果它们把所有相同的输入都映射到相同的输出，那从一个使用者的视角来看，这两个function就是等价的——我们在外部并不能观察到任何区别。同样地，我们也可以从这个角度定义schedule之间的等价关系，如果两个schedule在所有相同的数据库状态下执行都会使数据库转移到相同的最终状态，那它们对我们来说就是等价的。正式地说¹：

我们说两个schedule $S_1$ 和 $S_2$ 是 终态等价的（final state equivalent），如果它们满足：

• 它们涉及的transactions相同；以及
• 在所有对写操作的解读下（ $w_i(x)$ 可能是任何关于之前读取的数据的函数 $f$ ），对于所有的初始状态 $I$，$I\xrightarrow{S_1}I’\Leftrightarrow I\xrightarrow{S_2}I’$

我们可以相应地给出final state serializability的定义：

如果一个schedule $S=(\tau, \prec_S)$ final state equivalent to 某个serial schedule $S’=(\tau, \prec_{S’})$，那么 $S$ 就是final state serializable的。

这个定义非常直观，可是我们该怎么检查两个schedule是不是final state equivalent的呢？根据定义来检查肯定不现实，我们没法去检查每一种可能的初始状态，但是我们可以通过给schedule中的数据操作构建一个图来进行验证¹：

• 对于每个schedule $S$，定义一个 augmented schedule $\hat{S}$。$\hat{S}$ 除了包括 $S$ 中的所有transaction之外，还包含两个辅助transaction $T_0$ 和 $T_\alpha$:
  • $T_0$ 只有写操作，写入所有的object，相当于数据库中所有object的初始值；
  • $T_\alpha$ 只有读操作，读取所有的object，相当于数据库中所有object的最终值。
• $\hat{S}$ 保留 $S$ 中的操作的顺序，并保证 $T_0$ 在 $S$ 之前，$T_\alpha$ 在 $S$ 之后。（ $\hat{S}\equiv T_0~S~T_\alpha$ ）
• 根据这个augmented schedule $\hat{S}$，构建一个有向图 $D(S)=(V, E)$：
  • 节点 $V$ 是 $\hat{S}$ 中所有的数据操作（e.g., $r_i(x), w_j(y), \dots$）；
  • 边 $E$ 包含 $o_1\to o_2$，如果 $o_1\prec_{\hat{S}}o_2$，以及：
    • 在某个transaction $T_i$ 中，$o_1=r_i(x), o_2=w_i(x)$；或者
    • $o_1$ 和 $o_2$ 属于不同的transaction，并且 $o_2$ 从 $o_1$ 中读取（read from）。

我们说 $o_2$ 从 $o_1$ 中读取（ $o_2$ reads from $o_1$ ），如果：

• 对于某个数据对象 $x$，$o_1=w_i(x), o_2=r_j(x)$；并且
• $o_1\prec_S o_2$，并且 $o_1$ 和 $o_2$ 之间没有其他操作也写入了 $x$

举个例子，对于以下两个schedule $S_1, S_2$：

$S_1: r_2(x), w_2(x), r_1(x), w_1(y), w_2(y)$ 所对应的图 $D(S_1)$ 是：

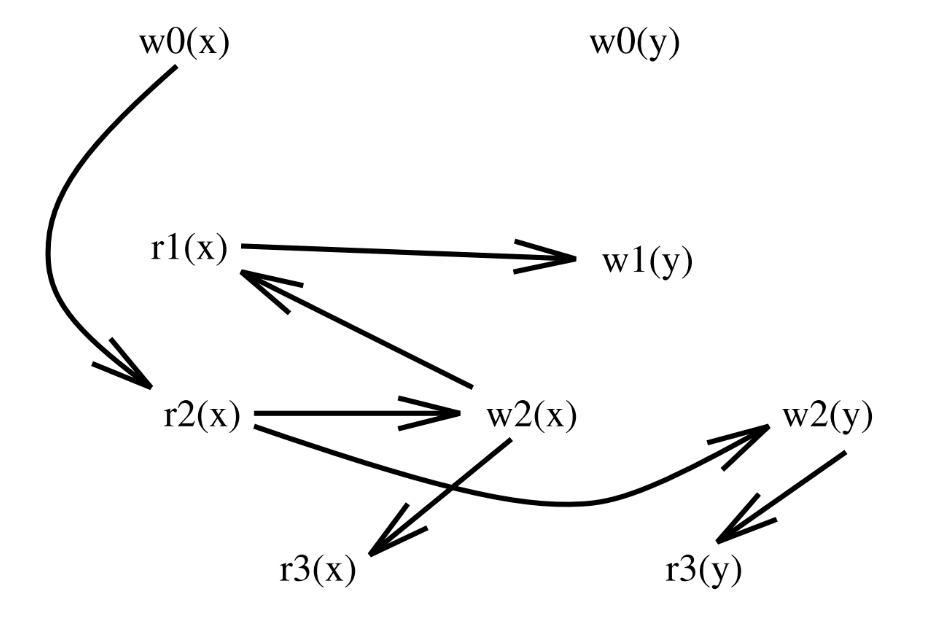
$S_2: r_1(x), w_1(y), r_2(x), w_2(x), w_2(y)$ 所对应的图 $D(S_2)$ 是：

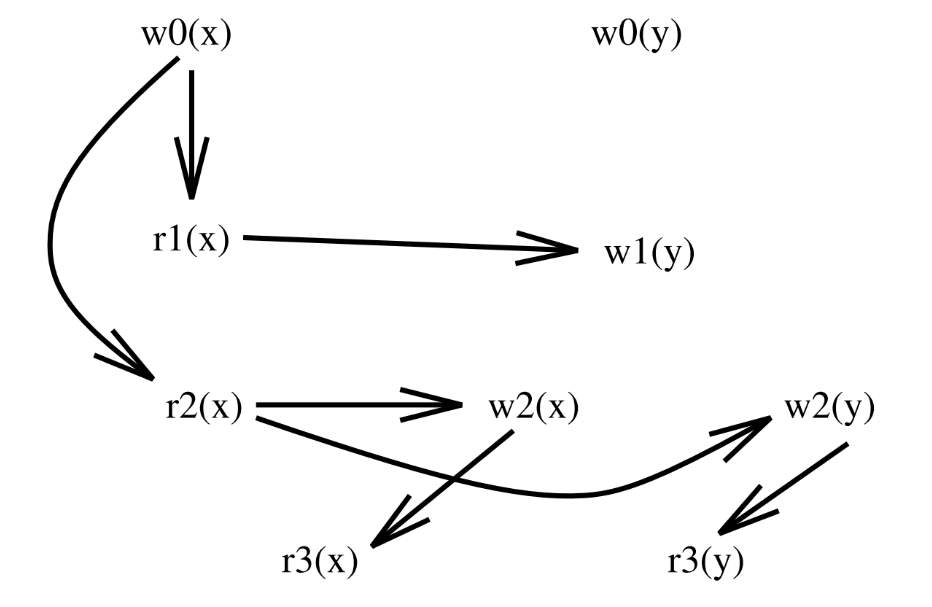
_{（例子及图片出自¹）}

仔细观察我们就会发现，$D(S)$ 实际上描述了信息是怎么在 $S$ 中“流动”的：$w_0(x)\to r_1(x)$ 代表了 $r_1$ 读取了 $w_0$，$x$ 的初始信息从 $w_0$ “流动”到了 $r_1$；$r_2(x)\to w_2(x)$ 代表了 $r_2$ 之后的 $w_2$ 可能用到了 $r_2$ 读取到的数据，信息从 $r_2$ “流动”并反映到了 $w_2$。所以，指向最终代表最终状态的 $r_\alpha$ 的path就代表了构成数据库最终状态的“信息流”。

综上所述，如果我们把 $D(S_1)$ 和 $D(S_2)$ 中所有无法达到 $r_\alpha(\cdot)$ 的节点都删除，并且得到的结果完全相同的话，那么 $S_1$ 和 $S_2$ 就是final state equivalent的：

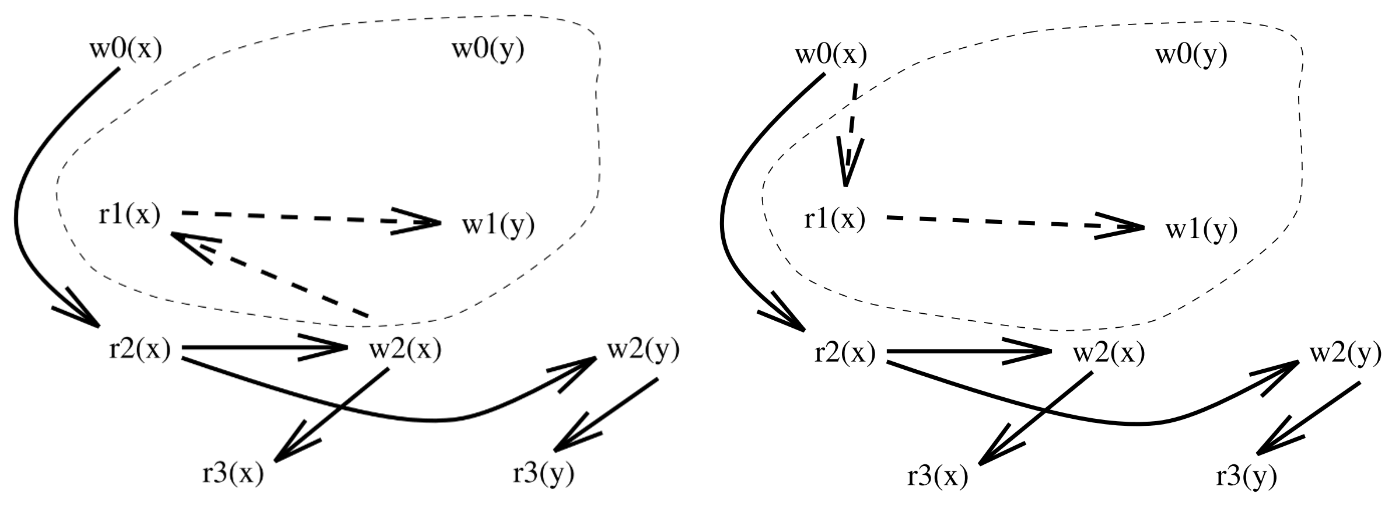
视域可串行（view serializability）

Final state serializability的定义看起来很简单也很合理，但是它本质上还是一种忽略了内部结构的external equivalence. 然而这种忽略在我们的模型中有时也会产生错误。比如我们有一个数据库 $d=\{x, y, z\}$，这个数据库的constraint是 $x=y\land z\ge 0$. 初始状态是 $\{x=5, y=5, z=2\}$。考虑如下的两个应用程序：

如果我们以 $S: w_2(z, -1), w_1(x, 7), r_2(x, 7), r_2(y, 5), w_1(y, 7)$ 来执行这两个程序，最终的状态是 $\{x=7, y=7, z=-1\}$，并不满足我们的constraint，data consistency被打破了。有趣的地方在于，$T_1$ 和 $T_2$ 以任意顺序串行执行都不会造成inconsistency；我们的schedule $S$ 也是final state serializable的（读者可以用上文介绍的方法自行验证），却产生了inconsistent的结果。

仔细观察后我们不难发现，造成这一现象的原因是，在final state serializability中，我们把transaction和schedule当成了黑盒，假设了数据库的状态仅仅取决于输出（写操作）的状态。但是从这个例子中我们可以看到，$T_2$ 中的读操作 $r_2(x)$ 和 $r_2(y)$ 也对状态产生了影响，因为我们的简化模型里并没有考虑到控制流等等同样会基于读取到的信息对输出产生影响的内部结构。

根据这个观察，如果我们也同时保证所有transaction“看到的”数据状态也等同于它们在sequential execution中所“看到的”状态，这个问题不就解决了吗？于是我们有了 view equivalence 和 view serializability 的定义¹⁴：

我们说两个schedule $S_1$ 和 $S_2$ 是 视域等价的（view equivalent），如果它们满足：

• 它们涉及的transactions相同；以及
• 对于 $S_1$ 和 $S_2$ 中的任意transaction $T_i$ 和 $T_j$，如果在 $S_1$ 中， $o_i\in T_i$ 从 $o_j\in T_j$ 中读取（read from），那么在 $S_2$ 中，$o_i$ 也 从 $o_j$ 中读取（read from）；以及
• 对于任意一个数据对象 $x$，如果在 $S_1$ 中 $T_i$ 最后写入了 $x$，那么在 $S_2$ 中 $T_i$ 也最后写入 $x$

相应地给出view serializability的定义：

如果一个schedule $S=(\tau, \prec_S)$ view equivalent to 某个serial schedule $S’=(\tau, \prec_{S’})$，那么 $S$ 就是view serializable的。

检查两个schedule $S_1, S_2$ 是否view equivalent的方法与检查final state equivalence的方法类似：构造出图 $D(S_1)$ 和 $D(S_2)$，但是因为这次我们同样关心每个操作所“看到”的状态是否一致，所以不能删除无法到达最终状态的节点。所以，如果 $D(S_1)$ 和 $D(S_2)$ 完全相同，那么 $S_1$ 和 $S_2$ 就是view equivalent的。显然，我们可以发现，view serializable的schedule也一定是final state serializable的，反之则不成立。

下面是一个view serializable的schedule的例子，$S\equiv T_2~T_1~T_3$，读者可以自行尝试验证：

冲突可串行（conflict serializability）

View serializability似乎一举解决了consistency的问题（也确实解决了⁴），但是判断一个schedule是不是view serializable却是一个NP-complete的问题⁴ 。这样的复杂度在现实世界的数据库系统中是不现实的，我们还需要一个更易于验证的serializability定义。

重新思考并发schedule造成inconsistency的原因，我们发现实际上关键仅仅在于某几个数据操作的顺序：在一个schedule中这些关键操作是这种顺序；在另一个schedule中可能是另一种顺序。这种顺序的区别导致了isolation的破坏和inconsistency。比如在我们最开始的银行转账的例子中，关键的 $w_A(x), r_B(x)$ 和 $w_A(y), r_B(y)$ 的执行顺序导致了 $T_B$ 读取了 $T_A$ 的partial effect. 如果我们确保在schedule $S$ 中，所有这样的关键操作的执行顺序都和某个serial schedule中这些操作的执行顺序相同，那么我们就可以保证consistency了。

那什么样的操作是关键操作呢？根据我们的观察，不满足“交换律”的操作就是这样的关键操作：$r_i(\cdot)$ 和 $r_j(\cdot)$ 是满足交换律的，任意一种执行顺序都会产生同样的效果；但是 $r_i(x)$ 和 $w_j(x)$、$w_i(x)$ 和 $w_j(x)$ 就不满足交换律，不同的顺序会产生不同的状态。所以我们定义 冲突操作（conflicting operations）¹：

两个数据操作 $o_i$ 和 $o_j$ 是一对 冲突操作（conflicting operations），如果它们满足：

• 它们属于不同的transaction；以及
• 其中至少一个操作是写操作。

由此，我们可以给出 conflict equivalence 和 conflict serializability 的定义¹⁴：

我们说两个schedule $S_1$ 和 $S_2$ 是 冲突等价的（conflict equivalent），如果它们满足：

• 它们涉及的transactions相同；以及
• 它们对 冲突操作（conflicting operations） 的排序相同。

相应地，

如果一个schedule $S=(\tau, \prec_S)$ conflict equivalent to 某个serial schedule $S’=(\tau, \prec_{S’})$，那么 $S$ 就是conflict serializable的。

检查一个schedule $S$ 是否conflict serializable非常简单：

• 根据 $S$ 构造一个有向图：串行化图（serialization graph） $SG(S)=(V, E)$：
  • 节点 $V$ 是 $S$ 中的transactions $\tau$；
  • 边 $E$ 包含 $T_i\to T_j$，如果 $T_i, T_j$ 中有一对conflicting operations $o_i\in T_i, o_j\in T_j$，并且 $o_i$ 在 $S$ 中早于 $o_j$（ $o_i\prec_S o_j$ )

需要注意的是，这个serialization graph和之前final state serializability和view serializability中用到的图不同，serialization graph以transaction为单位，实际上描述了存在conflict的transaction之间的执行顺序。我们可以发现，如果 $T_i\to T_j$ 是 $SG(S)$ 的一条边，意味着 $T_i$ 比 $T_j$ 先执行了某项不满足交换律、会导致冲突的操作，那么如果存在一个和 $S$ 等价的serial schedule $S’$，那么在 $S’$ 中 $T_i$ 也必定先于 $T_j$ 执行（ $T_i\prec_{S’}T_j$ ）。所以，如果serialization graph $SG(S)$ 中出现了一个环，那么 $S$ 肯定就不是conflict serializable的。

所以conflict serializability的判断可以通过判断一个schedule $S$ 的serialization graph $SG(S)$ 有没有环来完成，而检查一个图有没有环可以在 $O(|E|)$，或者说 $O(n^2)$ 时间完成。

如果一个schedule是conflict serializable的，它也一定是view serializable的，反之则不成立。所以conflict serializability实际上是牺牲了一部分的并发程度来使检验变得更容易。

后记

至此，我们建立了模型，从理论上分析了serializability的合理性，并通过三种不同的角度定义了三种不同的serializability：final state serializability、view serializability、和conflict serializability. 在现实应用中，final state serializability和view serializability要么存在正确性的问题，要么太过复杂难以实用，所以我们采用了放弃了一部分合法的schedule但是较为简单的conflict serializability.

作为高度抽象的理论分析，serializability这个概念本身也有一些局限性。比如它没有将实际运行的数据库应用或者服务的语境纳入考虑，如果我对“正确性”的要求没有达到serializable的程度呢？这就要求我们回到本文一开始的问题、更加细致地讨论究竟“正确”这个词意味着什么了。感兴趣的读者可以参考阅读 Correctness Criteria Beyond Serializability. ⁵

在这个系列之后（可能会有）的文章里，我们会继续关于serializability的旅程，介绍一些实现conflict serializability的算法，比如 two-phase locking；还有可能讨论讨论数据库系统中除consistency之外的需求，比如 recoverability 等等。

参考资料